435. 无重叠区间（贪心算法）

435. 无重叠区间

• 题目
• 解题思路
• 代码

题目

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意:

可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。

解题思路

先计算最多能组成的不重叠区间个数，然后用区间总个数减去不重叠区间的个数。得到的就是“需要移除区间的数量”。

在每次选择中，区间的结尾越小，留给后面的区间的空间越大，那么后面能够选择的区间个数也就越大，故而需要移除的区间数量就越小。

按区间的结尾进行排序，每次选择结尾最小，并且和前一个区间不重叠的区间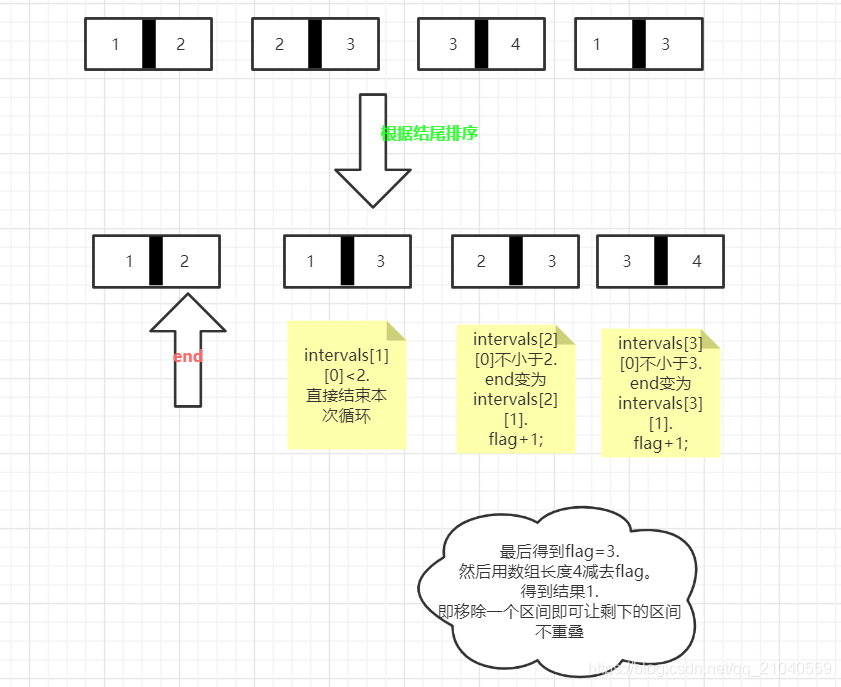

详情见书P383

代码

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        int n = intervals.length;

        //求出有n个区间不会重叠，剩下的区间就是需要去除的。
        return n - intervals(intervals);
    }

    /**
     * 最多有n个 区间不会重叠
     *
     * @param intervals
     * @return
     */
    public int intervals(int[][] intervals) {
        if (intervals.length == 0) {
            return 0;
        }
        Arrays.sort(intervals, new Comparator<int[]>() {
            @Override
            //按照end升序排列
            public int compare(int[] o1, int[] o2) {
                return o1[1] - o2[1];
            }
        });
        //至少有一个区间不相交,就是只有一个区间的时候
        int count = 1;
        //排序后第一个区间就是x
        int x_end = intervals[0][1];

        for (int[] interval : intervals) {
            int start = interval[0];
            if (start >= x_end) {
                //找到下一个选择的区间了
                count++;
                x_end = interval[1];
            }
        }
        return count;
    }
}