什么是安全序列

题目描述

如果B还要借30亿：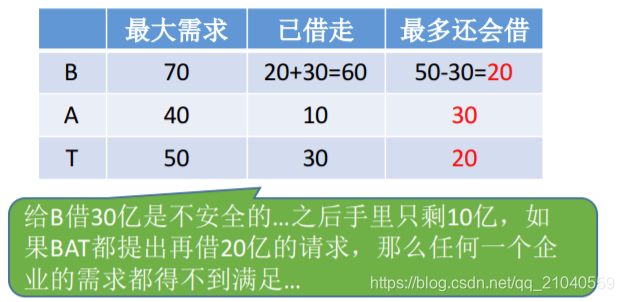
在这里插入图片描述

但是如果A要借20亿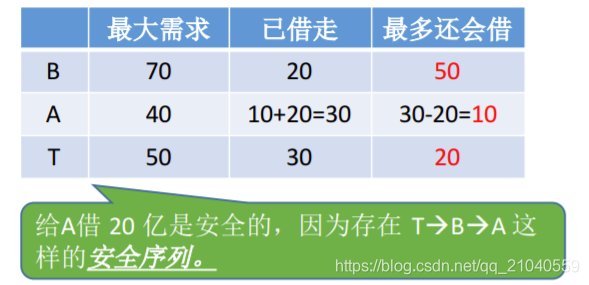
在这里插入图片描述

所谓安全序列,就是指如果系统按照这种序列分配资源,则每个进程都能顺利完成。只要能找出一个安全序列,系统就是安全状态。当然,安全序列可能有多个。

如果分配了资源之后,系统中找不出任何一个安全序列,系统就进入了不安全状态。这就意味着之后可能所有进程都无法顺利的执行下去。当然,如果有进程提前归还了一些资源,那系统也有可能重新回到安全状态,不过我们在分配资源之前总是要考虑到最坏的情况。

如果系统处于安全状态,就一定不会发生死锁。如果系统进入不安全状态，就可能发生死锁，（不安全状态未必就是发生了死锁,但发生死锁时一定是在不安全状态)
因此可以在资源分配之前预先判断这次分配是否会导致系统进入不安全状态,以此决定是否答应资源分配请求。这也是“银行家算法”的核心思想。

银行家算法

银行家算法是荷兰学者 Dijkstra为银行系统设计的,以确保银行在发放现金贷款时,不会发生不能满足所有客户需要的情况。后来该算法被用在操作系统中,用于避免死锁。

核心思想: 在进程提出资源申请时,先预判此次分配是否会导致系统进入不安全状态。如果会进入不安全状态,就暂时不答应这次请求,让该进程先阻塞等待。

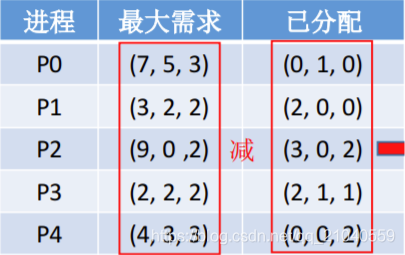
在这里插入图片描述
现在手里握着资源(10,5,7)，且有五个进程。（此时总共已分配(7,2,5),还剩余(3,3,2)。可把最大需求、已分配的数据看作矩阵两矩阵相减,就可算出各进程最多还需要多少资源了）。

然后计算出每个进程的最多还需要多少资源。然后和剩余资源作比较，看剩余资源能否满足。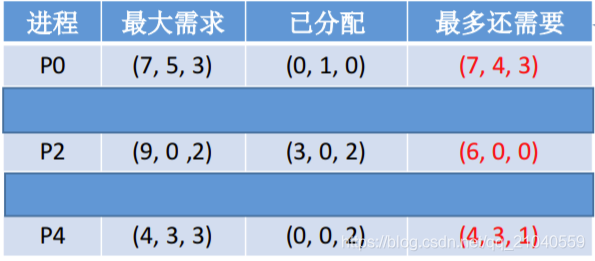
在这里插入图片描述
可以看出P1、P3的最多还需要的值是小于剩余资源(3,3,2)的，所以可以把P1、P3加入安全序列。

思路：
依次检査剩余可用资源(3,3,2)是否能满足各进程的需求。

可满足P1需求,将P1加入安全序列,并更新剩余可用资源值为(5,3,2)
首先我们P1还需要(1,2,2)，我们还有资源(3,3,2)，于是便用剩余资源减去需要资源得到：(2,1,0)。然后P1得到了所有资源就会归还占用的资源，所以现在剩余资源(2,1,0)+(3,2,2)=(5,3,2)

依次检査剩余可用资源(5,3,2)是否能满足剩余进程(不包括已加入安全序列的进程)的需求
可满足P3需求,将P3加入安全序列,并更新剩余可用资源值为(7,4,3)
依次检査剩余可用资源(7,4,3)是否能满足剩余进程(不包括已加入安全序列的进程)的需求

以此类推,共五次循环检査即可将5个进程都加入安全序列中,最终可得一个安全序列。该算法称为安全性算法。可以很方便地用代码实现以上流程,每一轮检査都从编号较小的进程开始检査。实际做题时可以更快速的得到安全序列。

实际做题(手算)时可用更快速的方法找到一个安全序列:
经对比发现,(3,3,2)可满足P1、P3,说明无论如何,这两个进程的资源需求一定是可以依次被满足的,因此P1、P3一定可以顺利的执行完,并归还资源。可把P1、P3先加入安全序列。
（2,0,0)+(2,1,1)+(3,3,2)=(7,4,3)
剩下的P0、P2、P4都可被满足。同理,这些进程都可以加入安全序列。
于是,5个进程全部加入安全序列,说明此时系统处于安全状态,暂不可能发生死锁。

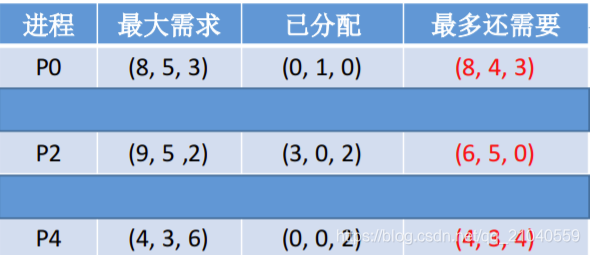
不安全的例子

再看一个找不到安全序列的例子:
经对比发现,(3,3,2)可满足P1、P3,说明无论如何,这两个进程的资源需求一定是可以依次被满足的,因此P1、P3一定可以顺利的执行完,并归还资源。可把P1、P3先加入安全序列。
（2,0,0)+(2,1,1)+(3,3,2)=(7,4,3)
剩下的P需要(8,4,3),P2需要(6,5,0),P4需要(4,3,4)
任何一个进程都不能被完全满足于是,无法找到任何一个安全序列,说明此时系统处于不安全状态,有可能发生死锁。

数据结构:
长度为m的一维数组 Available表示还有多少可用资源
n_m矩阵Max表示各进程对资源的最大需求数
n_m矩阵 Allocation表示已经给各进程分配了多少资源
Max- Allocation=Ned矩阵表示各进程最多还需要多少资源
用长度为m的一位数组 Request表示进程此次申请的各种资源数

银行家算法步骤:
①检查此次申请是否超过了之前声明的最大需求数
②检査此时系统剩余的可用资源是否还能满足这次请求
③试探着分配(只是改动数据，并没有真实的分配资源),更改各数据结构
④用安全性算法检查此次分配是否会导致系统进入不安全状态

安全性算法步骤:
检査当前的剩余可用资源是否能满足某个进程的最大需求,如果可以,就把该进程加入安全序列,并把该进程持有的资源全部回收。

不断重复上述过程,看最终是否能让所有进程都加入安全序列。