96. 不同的二叉搜索树（动态规划）

96. 不同的二叉搜索树

• 题目
• 解题思路
• 代码

题目

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

解题思路

当遇到一个题目是让你求最值的时候你就可以考虑用动态规划的方式来做。
这种解题模板:
①搞个简单点的例子，用枚举法写出所有情况
②找规律：找出状态转移方程
③优化dp数组的记录

比如这题可以理解为：最多有多少种不同的二叉搜索树，首先可以分析出来。假如有n个数1，2，3…i…n
我们取其中的i作为根节点的话，那么情况就是[1,i-1] i [i+1,n]
我们再用n=3来代替。则自己可以枚举出来：
①i=1：i左边有0个节点，即可以组成1种树（空树），i右边有2个节点，可以组成2种子树， 即1_2=2.
②i=2：i左边有1个节点，即可以组成1种树，i右边有1个节点，可以组成1种子树， 即1_1=1.
③i=3：i左边有2个节点，即可以组成2种树，i右边有0个节点，可以组成1种子树， 即2*1=2.
④将这几种情况加起来就是最终要求的结果，即f[n]=2+1+2=5；共有5种不同的二叉搜索树

把这题一抽象：即
f(根结点左边可能的结点个数)*f(根右边剩余可以放的结点个数)
即f(i-1)*f(n-i)：以i为根节点，其左右两边的子树组成数量相乘得到以i为根节点的所有二叉搜索树的数量

(f(i-1)*f(n-i))：对上一步求出来的结果求个和

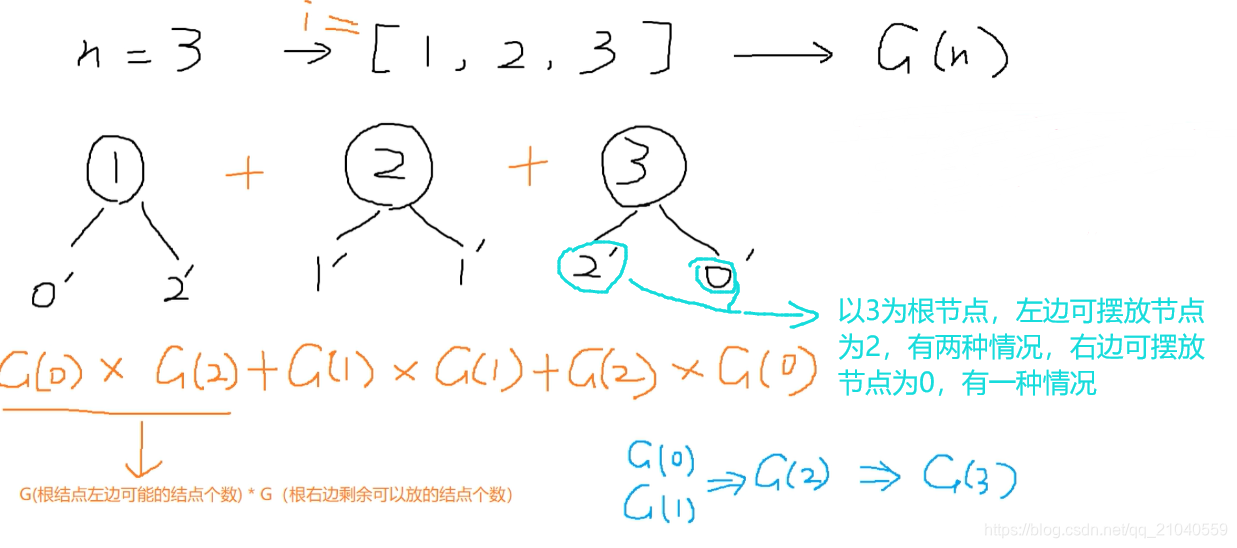
代码

class Solution {
    public int numTrees(int n) {
        int[] f = new int[n + 1];//长度是n+1是为了存放之前所有子结果的和
        f[0] = 1;//如果n是0，那么就是一种情况，空子树
        for (int i = 1; i <= n; i++) {//当i为节点的时候
            for (int j = 1; j <= i; j++) {//用二层循环是为了求出i左边和i右边的子树情况
                /*
                每一次都要将前一次的值和本次求出的结果求和再存入f，这样可以保证最后返回的f[n]是综合了所有情况的值

                这里把j看作根节点：
                    则j-1：就是根节点左边可以放的节点数，故而j-1个数可以组成f[j-1]种情况
                      i-j：就是根节点右边可以放的节点数，故而j-i个数可以组成f[j-i]种情况
                 */
                f[i] += f[j - 1] * f[i - j];//这里是把j作为根节点，i作为输入的数字

            }
        }
        return f[n];
    }
}