547. 朋友圈（DFS）

547. 朋友圈

• 题目
• 解题思路
• 代码

题目

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

提示：

• 1 <= N <= 200
• M[i][i] == 1
• M[i][j] == M[j][i]

解题思路

这题是可达性问题，用DFS来解决。
我们要注意一下，这题非常的诡异，虽然是个二维数组，但是题目却是要求以下标值作为人。
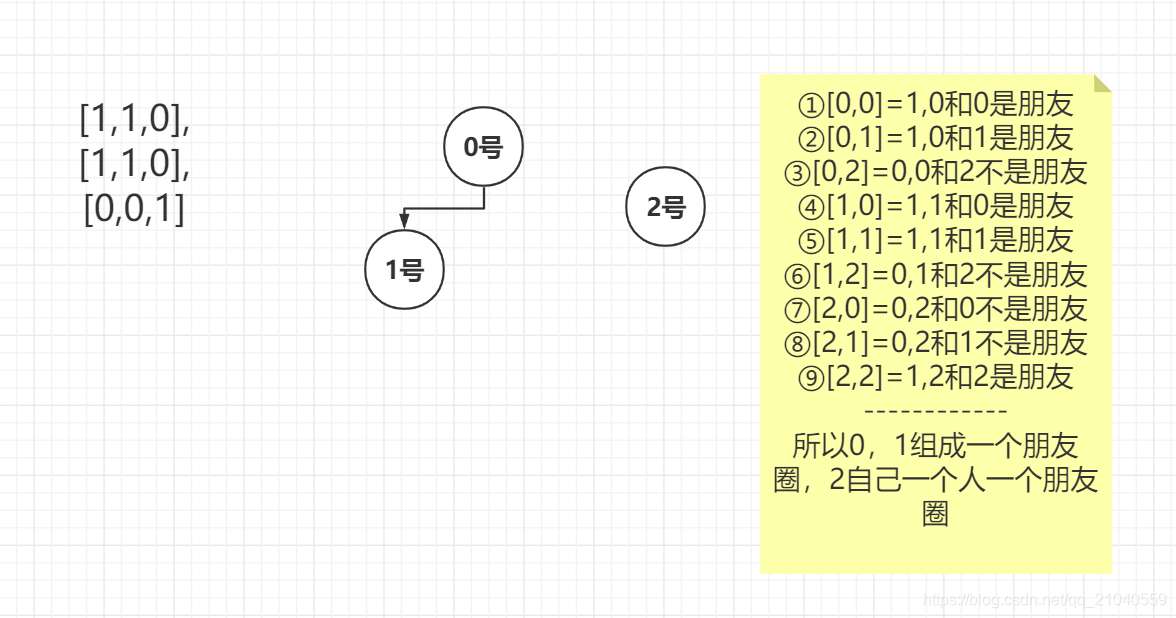
即M[0,0]=1代表0号人与它自己是朋友
M[0,1]=1代表0号人与1号人是朋友
M[1,2]=1代表1号人与2号人是朋友
但是友谊是可以传递的，1号和2号是朋友 所以0号和2号也是朋友

抓住这一点，我们就可以解决问题，我们第一次从0号人开始找，用DFS找到0号人的直接朋友。
然后再找0号人的直接朋友的朋友，一直用DFS找下去，直到遇到不是朋友的就返回。

代码

class Solution {
       public int findCircleNum(int[][] M) {
        boolean[] visited = new boolean[M.length];//会默认赋值为false
        int count = 0;
        for (int i = 0; i < M.length; i++) {//遍历整个人群
            if (visited[i] == false) {//如果i还没被访问过那么就去找i的朋友
                DFS(M, visited, i);
                count++;//i找完它的所有朋友就把count+1；接着再由i+1来找朋友
            }
        }
        return count;
    }


    public void DFS(int[][] M, boolean[] visited, int i) {
        visited[i] = true;

        for (int j = 0; j < M.length; j++) {
            if (visited[j] == false && M[i][j] == 1) {//如果j没被访问过，并且j是i的好朋友
                DFS(M, visited, j);
            }
        }


    }
}