687. 最长同值路径（递归）

文章目录

• 题目
• 解题思路
• 代码

题目

给定一个二叉树，找到最长的路径，这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。

注意：两个节点之间的路径长度由它们之间的边数表示。

解题思路

这题虽然题目说可不经过根节点，但是我们就以根节点出发。

我们只需要找到根节点的左子树的 相同值的 最长路径。和右子树的…。然后再把二者的长度加起来。

为了实现这个功能我们就需要一个辅助函数。
当然，如果类似于[1,2,3]这样的树，那么用辅助函数返回的左子树的和右子树的相同值最大路径就是0.即结果也是0.并不会影响最终结果。

这里在着重解释一下辅助函数的返回值的意思。

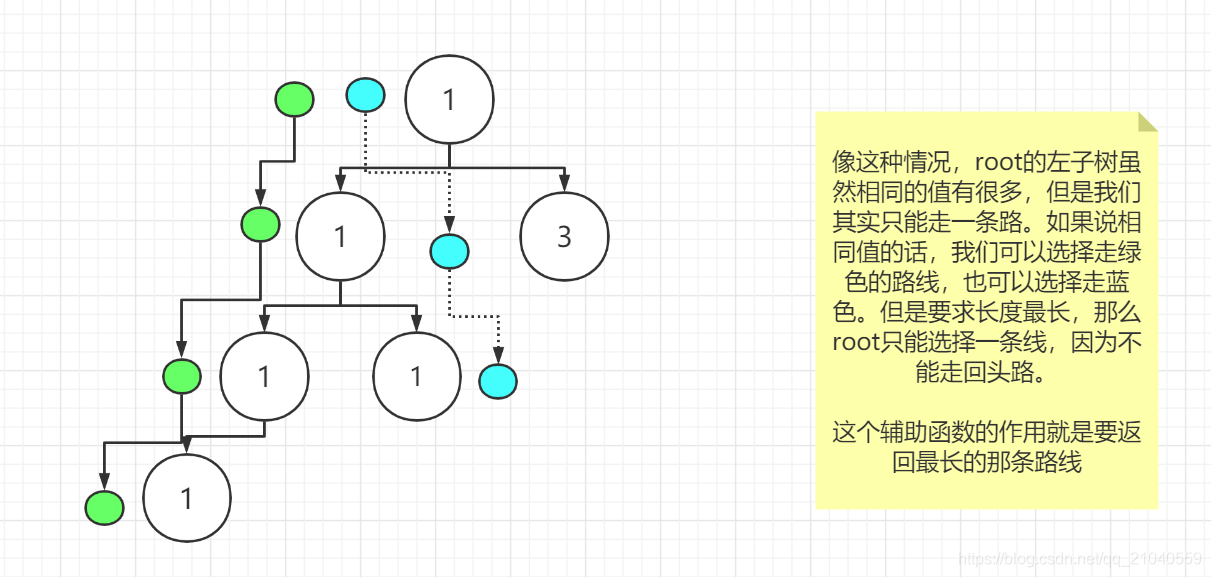
代码

class Solution {
    int res=0;
    public int longestUnivaluePath(TreeNode root) {
        help(root);
        return res;
    }

    public int help(TreeNode root){
        /*
        这个方法的功能就是，我传过来是左子树的时候，返回给我一个左子树的最长路径的最大值。
        用在右子树的时候同理。
        */


        if(root==null){
            return 0;
        }
        int leftCount=help(root.left);//用来保存左子树的最长路径的最大值
        int rightCount=help(root.right);//用来保存右子树的最长路径的最大值
        int left=0,right=0;//对于root来说，分别保存root左/右子树的最长路径

        if(root.left!=null&&root.left.val==root.val){//root的左子树不为空且值和root相同
            left=leftCount+1;//那么对于root来说左子树的最长路径就要+1
        }
        if(root.right!=null&&root.right.val==root.val){//root的右子树不为空且值和root相同
            right=rightCount+1;//那么对于root来说右子树的最长路径就要+1
        }

        res=Math.max(res,left+right);//注意！！更新结果在这里。对根节点来说，最长相同路径那就是左子树最长路径+右子树最长路径（假如右子树没有相同值那么right就是0，不影响最终结果）。用res来维护最大值

        return Math.max(left,right);//这个方法不用更改res，因为这个方法的目的是为了找出子树最长路径的最大值。 具体什么意思见CSDN

    }
}