题目

假设你有一个特殊的键盘包含下面的按键：

Key 1: (A)：在屏幕上打印一个 'A'。

Key 2: (Ctrl-A)：选中整个屏幕。

Key 3: (Ctrl-C)：复制选中区域到缓冲区。

Key 4: (Ctrl-V)：将缓冲区内容输出到上次输入的结束位置，并显示在屏幕上。

现在，你只可以按键 N 次（使用上述四种按键），请问屏幕上最多可以显示几个 ‘A’呢？

样例 1:
输入: N = 3
输出: 3
解释: 
我们最多可以在屏幕上显示三个'A'通过如下顺序按键：
A, A, A
 
样例 2:
输入: N = 7
输出: 9
解释: 
我们最多可以在屏幕上显示九个'A'通过如下顺序按键：
A, A, A, Ctrl A, Ctrl C, Ctrl V, Ctrl V

注释:
1 <= N <= 50
结果不会超过 32 位有符号整数范围。

解题思路

①确定状态，也就是变化的量，本题应该有三个状态，屏幕上A的数量、剪贴板中A的数量，按键次数N。这题为了dp数组的简单，就选择一个状态， 按键次数N。

②其实我们的最优按键序列只有两种情况：

要么一直按A
要么A,A,…,C-A,C-C,C-V…（当N比较大的时候）

用一句话来概括就是，最后一次要么按A，要么按C-V。这就是两种情况了

③定义dp[ ]：dp[N] 代表N次按键后A的数量

④对于按A，统计A的个数好说，但是对于按C-V，我们就需要用一个变量j来记录一下上一次按C-A,C-C的时机。

⑤现在大题思路都出来了，只需要记录按A键的A个数，然后遍历C-A,C-C的时机，在该时机下按C-V后A的个数，选取二者较大的那个即可。

看个图就明白了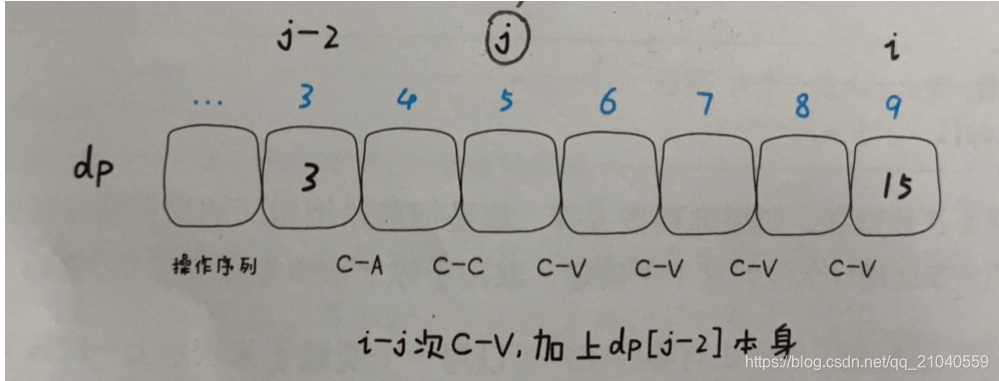
在这里插入图片描述

这里解释一下按下C-V后A的个数dp[j \- 2] * (i \- j + 1)：
按下C-V后，就是把剪贴板中的A的个数dp[j \- 2]乘以按下C-V的次数i-j。
但是为啥要加一个1呢？
因为我们求出的dp[j \- 2]*(i-j)只是按下C-V后出现的A，而屏幕上的A的个数是按下C-V后的A的个数dp[j \- 2]*(i-j)，加上屏幕上原来存在的A的个数dp[j-2]，才是屏幕上最终的A的数量

代码

 class solution{

    public int maxA(int N) {
        //dp[N] 代表N次按键后A的数量
        int dp[] = new int[N + 1];//长度为N+1是为了填入base case dp[0]=0
        //base case
        dp[0] = 0;

        for (int i = 1; i <= N; i++) {
            //此次按的是A键,那么产生的A就是上次的A数量加1
            dp[i] = dp[i - 1] + 1;
            /*用j来保存上一次按完C-A,C-C的时机，此时剪贴板中A的个数就是dp[j-2]
            因为  比如按键顺序如下A,A,A,C-A,C-C。j=5，但是A的数量为dp[j-2]=dp[3]。

            下面j从2开始也是同理。因为要有dp[j-2]所以j必须大于等于2才会让j-2始终大于等于0
            也可以理解为就是第一次按键就是C-A,C-C那也要两次按键。
             */
            for (int j = 2; j < i; j++) {
                //选出按A键，和按C-A,C-C后再按C-V键那个A数量多。
                dp[i] = Math.max(dp[i], dp[j - 2] * (i - j + 1));
            }
        }

        return dp[N];
    }
}