题目

你将获得 K 个鸡蛋，并可以使用一栋从 1 到 N 共有 N 层楼的建筑。

每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。

你知道存在楼层 F ，满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。

每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <= X <= N）。

你的目标是确切地知道 F 的值是多少。

无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少？
在这里插入图片描述

解题思路

①这题的状态有两个，一个是拥有的鸡蛋数K，还有进行测试的楼层N，所以我们的dp数组，或者是dp函数需要两个变量。这题是用的dp函数+备忘录的方式，所以要给dp函数多传递一个memo备忘录参数。 dp(K,N,memo)：在当前状态为K个鸡蛋面对N层楼，返回这个状态下的最少丢鸡蛋的次数

②base case：1、只有一个鸡蛋，只能线性扫描所有楼层。2、楼层为0，不需要扔鸡蛋

③现在就要找出状态转移方程。可以发现一个鸡蛋被丢出去就两种情况，碎或者没碎，我们就根据鸡蛋是否碎，来确定要搜索的楼层。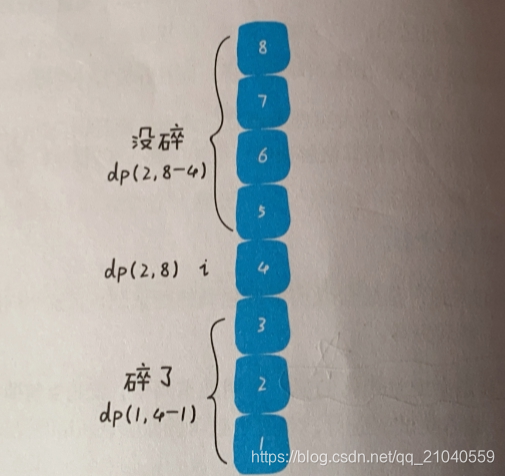
在这里插入图片描述

如果鸡蛋碎了,那么鸡蛋的个数K应该减一,搜索的楼层区间应该为[1..i-1]
如果鸡蛋没碎,那么鸡蛋的个数K不变,搜索的楼层区间应该变为[i+1...N]
注意:在第i层楼扔鸡蛋如果没碎,楼层的搜索区间缩小至上面的楼层,是不是应该包含第i层楼? 不必,因为已经包含了。题目说过楼层F可以为0，那么向上递归的时候第i层楼就相当于第0层，可以被抽取到。
还要注意，只有鸡蛋没碎才会有上面的疑问，因为没碎可能就是目标楼层，碎了一定不是目标楼层，根本不用再被抽取

④根据上面的思路已经可以写出第一版本的代码，但是加了备忘录在运行的时候还是会出现超时的现象，这就需要用到二分搜索法来优化。

dp(K-1,i-1)、dp(K,N-i)这两个函数，其中i是单调递增的，我们固定K和N，那么作出这个函数关于i的图像。根据i就可以知道两个函数的单调性。
那么这个交点就是我们要求的值，相当于求二分搜索中的valley（山谷）
只要在超时的代码中改进一下就可以了，下面我会贴出来超时的代码

代码

class Solution {
    public int superEggDzrop(int K, int N) {
        int[][] memo = new int[K + 1][N + 1];
        for (int[] item : memo) {//初始化一下备忘录，方便判定一下res是否存在于备忘录中
            Arrays.fill(item, -1);
        }
        return dp(K, N, memo);
    }

    public int dp(int K, int N, int[][] memo) {

        //base case
        if (K == 1) {//只有一个鸡蛋，只能线性扫描所有楼层
            return N;
        }
        if (N == 0) {//楼层为0，不需要扔鸡蛋
            return 0;
        }

        if (memo[K][N] != -1) {//备忘录有记录
            return memo[K][N];
        }

        int res = Integer.MAX_VALUE;
        int lo = 1;
        int hi = N;
        while (lo <= hi) {
            int mid = (lo + hi) / 2;
            int broken = dp(K - 1, mid - 1, memo);//鸡蛋碎了
            int not_broken = dp(K, N - mid, memo);//鸡蛋没碎

            //res=min(max(碎,没碎)+1);被分解成了下面两个 res
            if (broken > not_broken) {//没碎的函数在碎了的函数之上
                hi = mid - 1;//要靠近两函数交点，必须要缩小hi
                res = Math.min(res, broken + 1);//+1是因为在当前楼层扔鸡蛋，所以也要加一次次数
            } else {//碎的函数在没碎的函数之上
                lo = mid + 1;//要靠近两函数交点，必须要增大lo
                res = Math.min(res, not_broken + 1);
            }
        }
        memo[K][N] = res;
        return res;
    }
}

-———————————————->>

   /**
     * 用这种方法在K:6 N:5000的时候会超出时间限制，需要优化
     * @param K
     * @param N
     * @return
     */
    public int superEggDrop(int K, int N) {
        int[][] memo = new int[K + 1][N + 1];
        for (int[] item : memo) {//初始化一下备忘录，方便判定一下res是否存在于备忘录中
            Arrays.fill(item, -1);
        }
        return dp(K, N, memo);
    }

    public int dp(int K, int N, int[][] memo) {

        //base case
        if (K == 1) {//只有一个鸡蛋，只能线性扫描所有楼层
            return N;
        }
        if (N == 0) {//楼层为0，不需要扔鸡蛋
            return 0;
        }

        if (memo[K][N] != -1) {//备忘录有记录
            return memo[K][N];
        }

        int res = Integer.MAX_VALUE;
        for (int i = 1; i <= N; i++) {//i代表楼层
            res = Math.min(res, Math.max(dp(K - 1, i - 1, memo), dp(K, N - i, memo)) + 1);
        }
        memo[K][N] = res;
        return res;
    }