剑指 Offer 07. 重建二叉树

剑指 Offer 07. 重建二叉树

• 解题思路
• 代码

解题思路

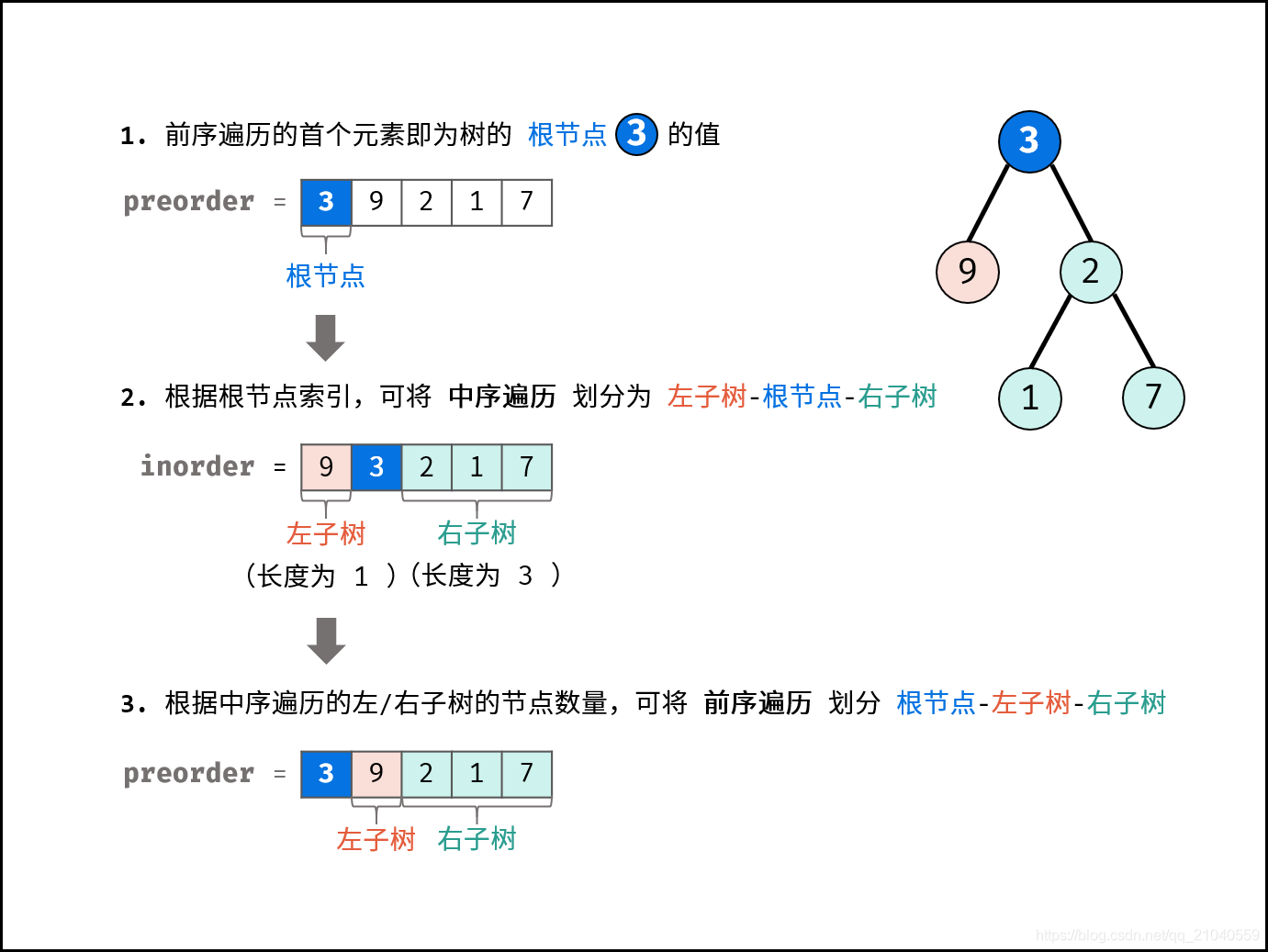
通过以上三步，可确定 三个节点 ：1.树的根节点、2.左子树根节点、3.右子树根节点。
对于树的左、右子树，仍可使用以上步骤划分子树的左右子树。

以上子树的递推性质是 分治算法 的体现，考虑通过递归对所有子树进行划分。

详细思路看注释即可

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    HashMap<Integer, Integer> map = new HashMap<>();//标记中序遍历
    int[] preorder;//保留的先序遍历

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        for (int i = 0; i < inorder.length; i++) {
            //将中序遍历的值及索引放在map中，方便递归时获取左子树与右子树的数量及其根的索引
            map.put(inorder[i], i);
        }
        /*三个索引分别为
        当前根的的索引
        递归树的左边界，即数组左边界
        递归树的右边界，即数组右边界*/
        return recursive(0, 0, inorder.length - 1);
    }

    TreeNode recursive(int pre_root, int in_left, int in_right) {
        if (in_left > in_right) {//越界了
            return null;// 相等的话就是自己
        }
        TreeNode root = new TreeNode(preorder[pre_root]);//获取root节点
        int idx = map.get(preorder[pre_root]);//获取在中序遍历中根节点所在索引，以方便获取左子树的数量

        //左子树的根的索引为先序中的根节点+1
        //递归左子树的左边界为原来的中序in_left
        //递归左子树的右边界为中序中的根节点索引-1
        root.left = recursive(pre_root + 1, in_left, idx - 1);
        //右子树的根的索引为先序中的 当前根位置 + 左子树的数量 + 1
        //递归右子树的左边界为中序中当前根节点+1
        //递归右子树的有边界为中序中原来右子树的边界
        root.right = recursive(pre_root + (idx - in_left) + 1, idx + 1, in_right);
        return root;

    }
}