剑指 Offer 60. n个骰子的点数

剑指 Offer 60. n个骰子的点数

• 解题思路
• 代码

解题思路

解题前须知

本题可用动态规划求解
1、我们先建立二维 dp 数组，dp[n][s] 表示投掷 n 个骰子，n 个朝上的面的点数之和为 s 的事件出现的次数。

2、那么动态转移方程就是：dp[n][s] += dp[n \- 1][s \- k]，k 属于 [1, 6]

• 我们可以举个例子来理解，假如 n = 3, s = 8，那么 dp[3][8] 表示投掷 3 个骰子，3 个朝上的面的点数之和为 8 的事件出现的次数。那么我们可以把求 dp[3][8] 转移为求只投掷 2 个骰子，2 个朝上的面的点数之和分别为 7、6、5、4、3、2 的事件的次数之和。
• 因为假如 “只投掷 2 个骰子，2 个朝上的面的点数之和为 7”，那么我们只需要再投一个骰子，让它的点数是 1，不就满足了 dp[3][8] 了嘛！
• 又比如 “只投掷 2 个骰子，2 个朝上的面的点数之和为 6”，那么我们只需要再投一个骰子，让它的点数是 2，不就满足了 dp[3][8] 了嘛！
• 依次类推

3、当然，上面的动态转移方程的前提条件是要保证 s - k > 0，因为没有骰子能投掷出小于等于 0 的点数。

代码

class Solution {
    public double[] dicesProbability(int n) {
        if (n <= 0) {
            return new double[0];
        }
        /*
        首先为了方便表达（dp[0][0]是没有含义的），我们将 dp 数组的行的数量设为 n + 1，列的数量设为 6n + 1。
        行表示 n，列表示 s，且 s 的最大值是 6n。
         */
        //dp[n][s] 表示投掷 n 个骰子，n 个朝上的面的点数之和为 s 的事件出现的次数
        int[][] dp = new int[n + 1][6 * n + 1];

        /*
            初始化 一颗骰子的情况.
            一颗骰子， s 的每个值可能出现的次数都为 1
        */
        for (int i = 1; i <= 6; i++) {
            dp[1][i] = 1;
        }

        for (int i = 2; i <= n; i++) {//表示骰子的个数
            for (int s = i; s <= 6 * i; s++) {//表示可能会出现的点数之和
                for (int j = 1; j <= 6; j++) {//表示当前这个骰子可能掷出的点数
                    if (s - j > 0) {//没有骰子能投掷出小于等于 0 的点数
                        dp[i][s] += dp[i - 1][s - j];//当前n个骰子出现的点数之和等于n-1个骰子出现的点数之和加上这一个出现的点数
                    } else {
                        break;
                    }
                }
            }
        }
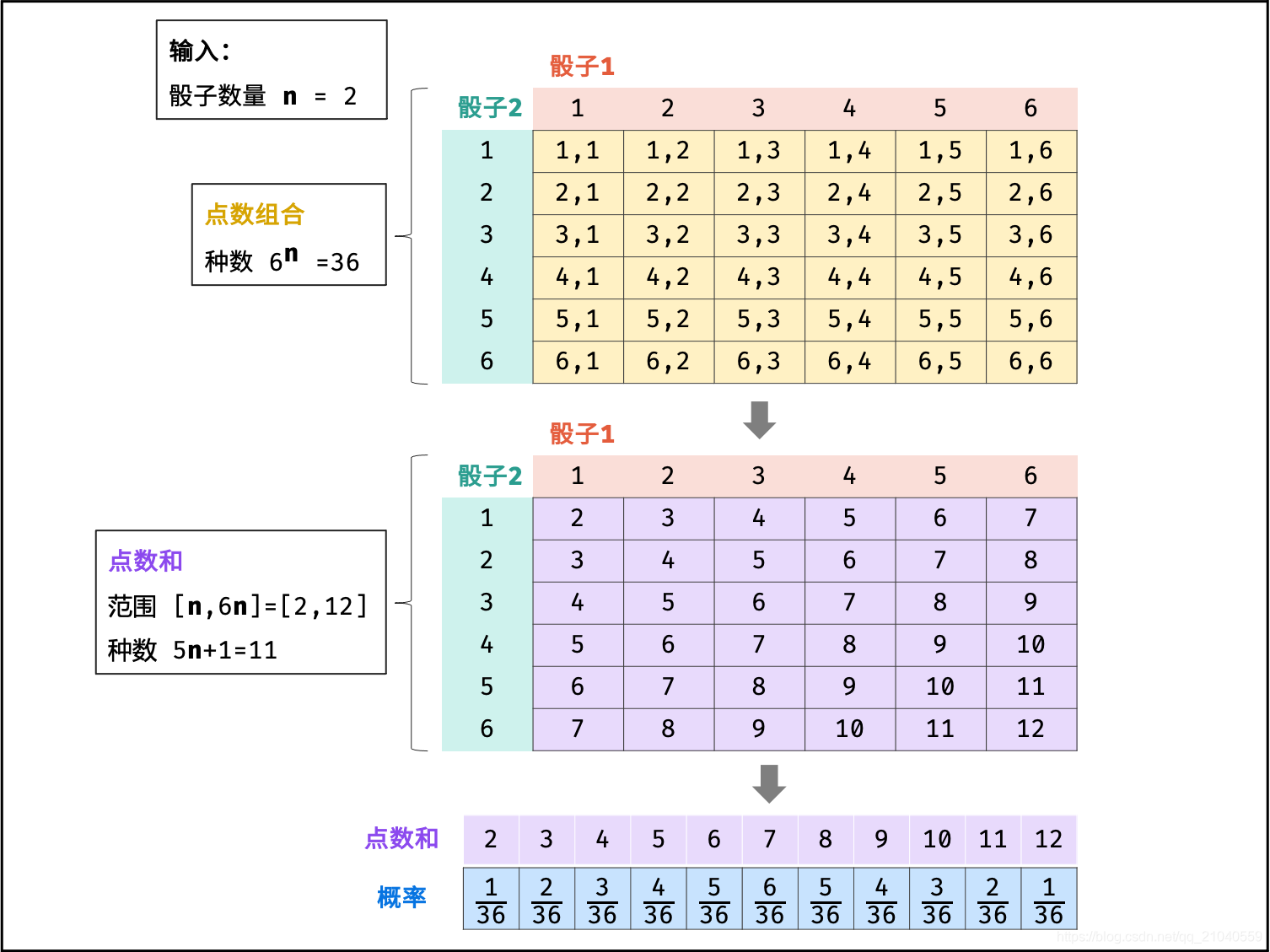
        double total = Math.pow((double) 6, (double) n);//有多少种点数配对情况，比如两骰子有6²=36种配对情况，也即骰子出现的和的次数为36次
        double[] ans = new double[5 * n + 1];//n个骰子「点数和」的范围为 [n, 6n] ，数量为 6n - n + 1 = 5n + 1 种。
        for (int i = n; i <= 6 * n; i++) {
            ans[i - n] = ((double) dp[n][i]) / total;//第i小的点数出现的概率
        }
        return ans;
    }
}