Dijkstra算法

Dijkstra算法

• 适用场景
• 算法流程
• 落地实现需要的数据结构

适用场景

单源最短路问题可以使用 Dijkstra 算法。例如lc743.网络延迟时间

算法流程

1. 首先，Dijkstra 算法需要从当前全部未确定最短路的点中，找到距离源点最短的点 x。
2. 同时标记x为下次的出发点，并且更新源点到其它点的距离
3. 当全部其他点都遍历完成后，一次循环结束，将 x 标记为已经确定最短路。进入下一轮循环，直到全部点被标记为确定了最短路。

举例

---

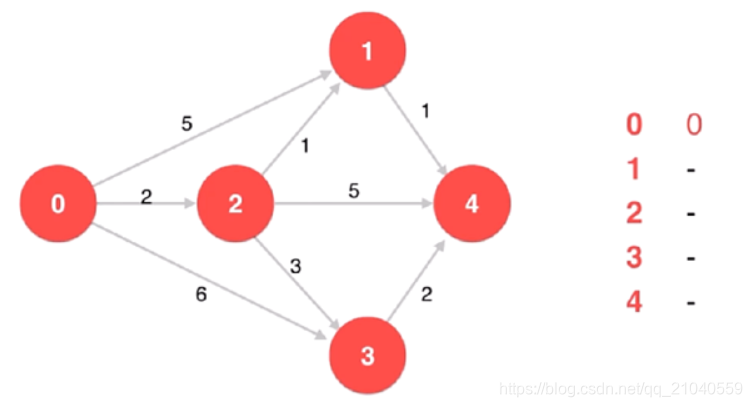
⬇️将顶点 0 进行标识，并作为点 xx，更新其到其他所有点的距离。一轮循环结束。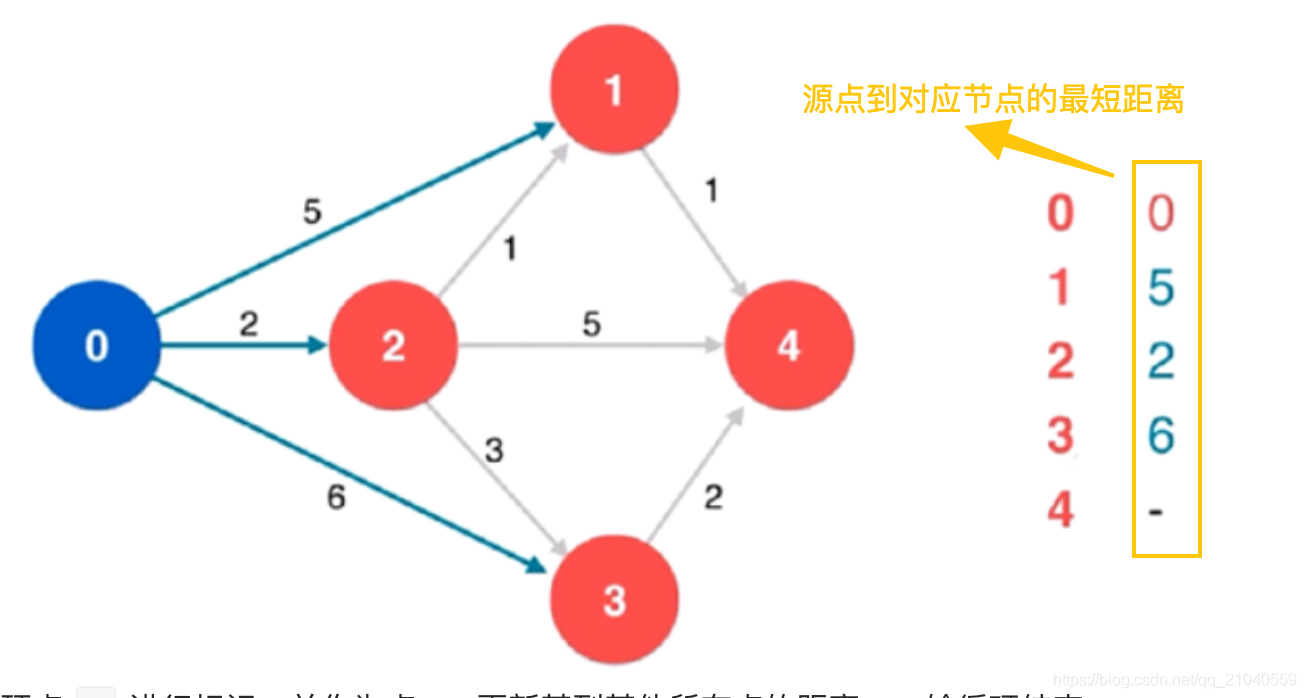

⬇️将顶点 2 进行标识，并作为新的点 x，更新。我们看到，原本 源点到点 1 的最短距离为 5，被更新为了 3。同理还更新了点 3 和点 4 的最短距离。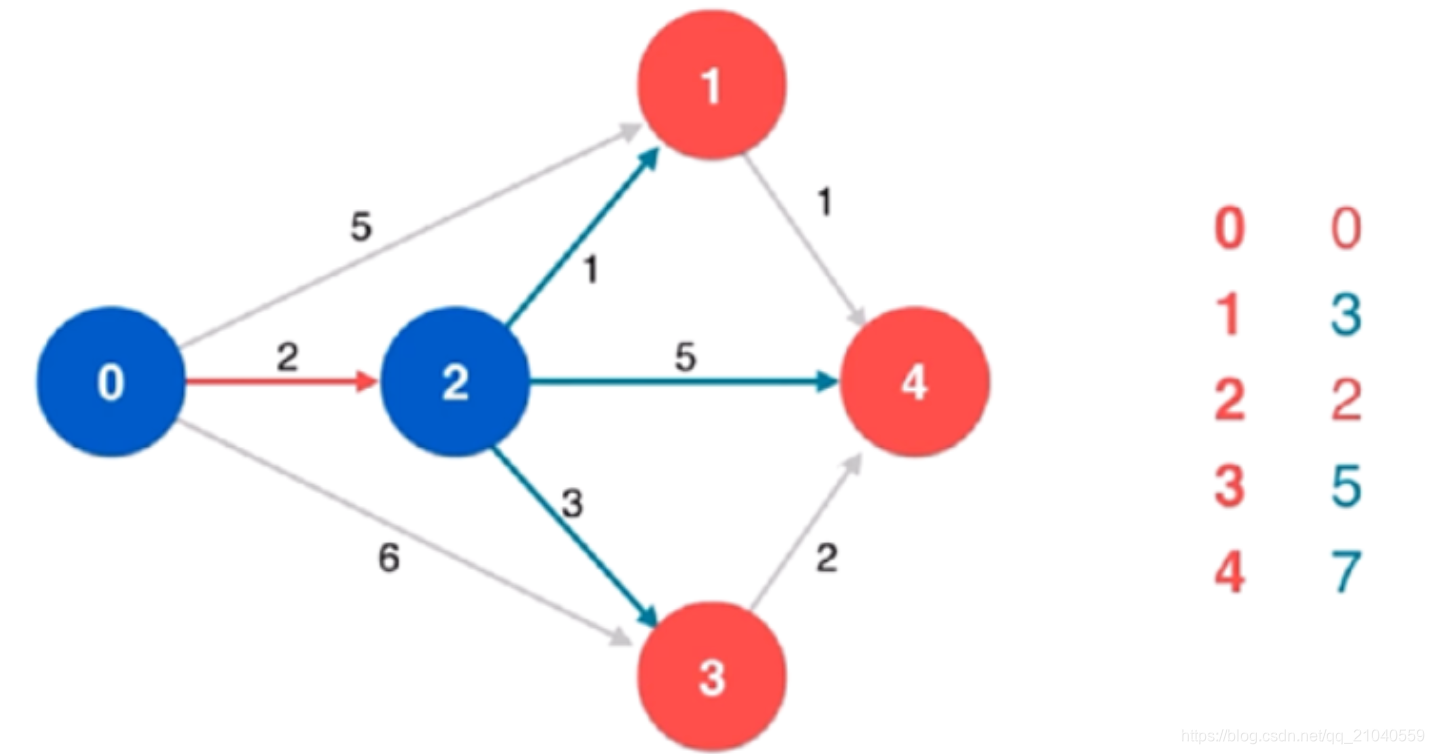

⬇️将顶点 1 进行标识，并作为新的点 x，同样更新了点 4 到源点的最短距离。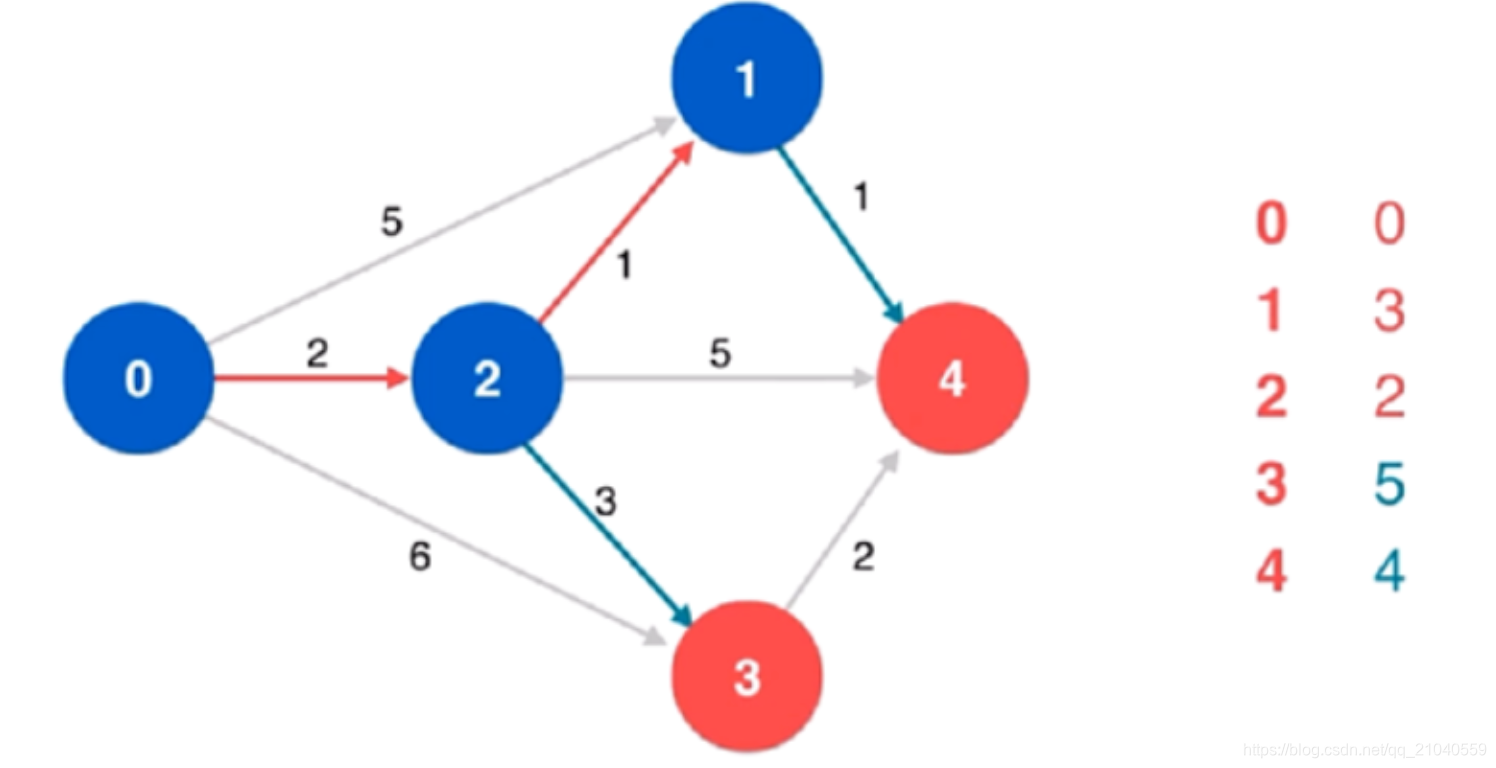

⬇️再分别标识点 4 和点 3，循环结束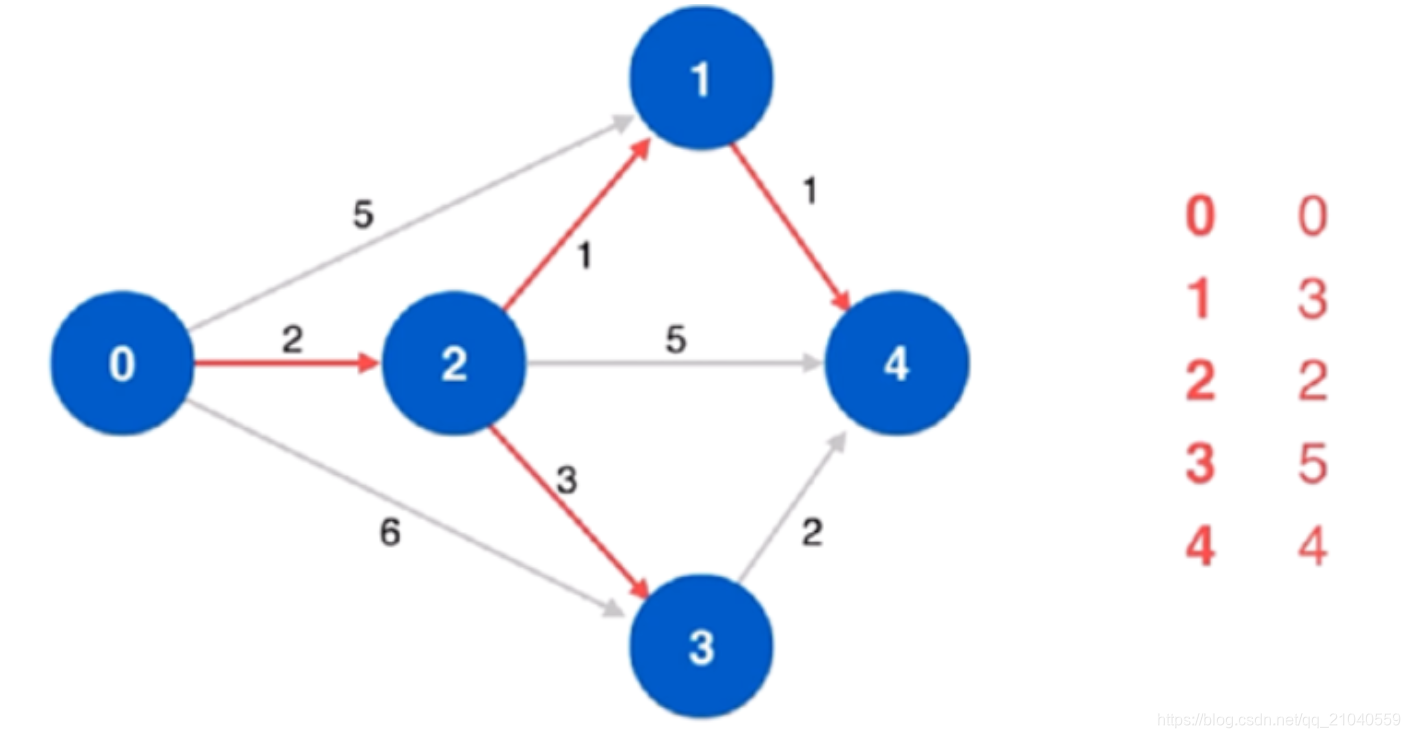

落地实现需要的数据结构

1. 首先，Dijkstra 算法需要存储各个边权，所以代码中使用了邻接矩阵g[i][j] 存储从点 i 到点 j 的距离。
2. 算法还需要记录所有点到源点的最短距离，代码中使用了 dist[i]数组存储源点到点 i 的最短距离
3. 算法需要标记某一节点是否已确定了最短路，代码中使用了 used[i]数组存储，若已确定最短距离，则值为 true，否则值为 false。

inf作为一个默认值，g[i][j]没有给出有向边的时候进行初始化。设置为 INT_MAX / 2，是因为在更新最短距离的时候，要有两个距离相加，为了防止溢出 int 型，所以除以 2